KoreanHackerTeam
Moderator
DES弱加密之easy_BlockCipher
첨부 파일을 다운로드하고 2 개의 파일을 가져옵니다.des-o-ofb.py:
Crypto에서 Cipher Import Des
f=open ( 'key.txt', 'r')
Key_Hex=F.Readline () [:-1] # Newline 버려집니다
f.close ()
key=key_hex.decode ( 'hex')
iv='13245678'
a=des.new (key, des.mode_ofb, iv)
f=Open ( 'PlainText', 'r')
PlainText=F.Read ()
f.close ()
ciphertext=a.encrypt (일반 텍스트)
f=open ( 'ciphertext', 'w')
F.Write (ciphertext)
F.close ()는 DES 알고리즘이 암호화 중에 사용되며 일반 텍스트는 OFB 모드로 암호화되어 있음을 보여줍니다.
따라서 알려진 IV=‘12345678’의 경우 암호 텍스트를 깨뜨리는 열쇠 만 알아야합니다.
알려진 정보에 따르면 IV와 알 수없는 키 만 있으므로 DES 암호화에 약한 키가 있다고 생각됩니다. DES 계산에서 56 비트 키는 결국 16 개의 라운드 키로 처리되며 각 라운드 키는 16 라운드 계산에 1 라운드에 사용됩니다. DES 약한 키는이 16 개의 라운드 키를 완전히 일관성있게 만들므로 약한 키라고합니다.
약한 키 중 4 개는 다음과 같습니다.
0x00000000000000000
0xfffffffffffffffffffffffffffffff
0xe1e1e1e1e1f0f0f0f0
0x1e1e1e1e1e0f0f0f0f는 4 개의 키 세트를 사용하여 암호 텍스트를 깨뜨립니다.
Crypto에서 Cipher Import Des
f=open ( 'ciphertext', 'r')
ciphertext=f.read ()
f.close ()
iv='13245678'
key=b '\ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00'
a=des.new (key, des.mode_ofb, iv)
일반 텍스트=a.decrypt (ciphertext)
일반 텍스트를 인쇄하십시오
key=b '\ x1e \ x1e \ x1e \ x1e \ x0f \ x0f \ x0f \ x0f \ x0f'
a=des.new (key, des.mode_ofb, iv)
일반 텍스트=a.decrypt (ciphertext)
일반 텍스트를 인쇄하십시오
key='\ xe1 \ xe1 \ xe1 \ xe1 \ xf0 \ xf0 \ xf0 \ xf0 \ xf0'
a=des.new (key, des.mode_ofb, iv)
일반 텍스트=a.decrypt (ciphertext)
일반 텍스트를 인쇄하십시오
key='\ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff'
a=des.new (key, des.mode_ofb, iv)
일반 텍스트=a.decrypt (ciphertext)
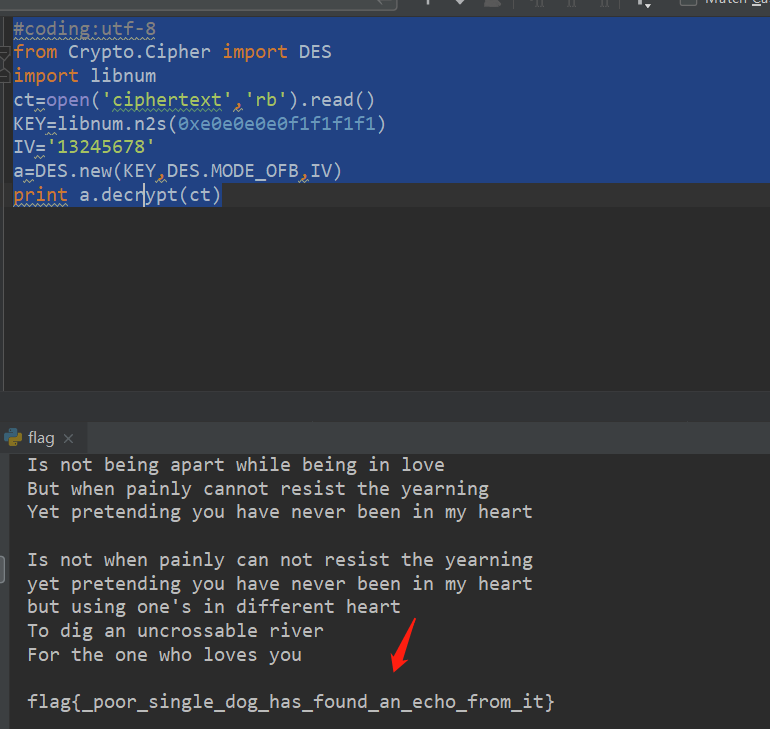
얻은 결과에서 일반 텍스트 인쇄는 셰익스피어의시입니다.
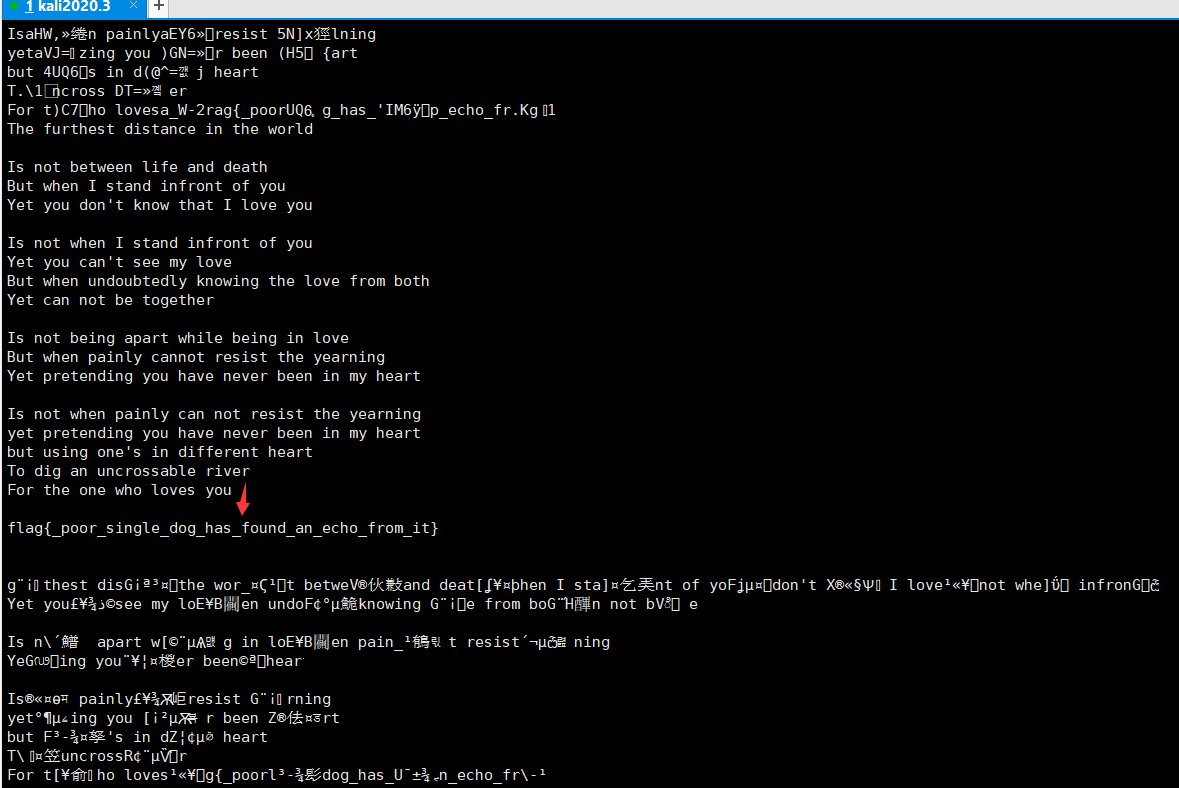
Crypto에서 Cipher Import Des
수입 libnum
ct=Open ( 'ciphertext', 'rb'). read ()
key=libnum.n2s (0xe0e0e0e0e0f1f1f1f1)
iv='13245678'
a=des.new (key, des.mode_ofb, iv)
A.Decrypt (CT)
RSA算法之special-rsa
질문 설명 : RSA 알고리즘을 학습 할 때 RSA와 동일한 보안이있는 알고리즘을 발견했습니다. 암호화 msg.txt는 msg.enc를 얻습니다. $ python special_rsa.py enc msg.txt msg.enc flag.enc에서 flag.txt를 복구 할 수 있습니까? 다음과 같이 4 개의 파일을 포함하는 첨부 파일을 다운로드하십시오.Special_rsa.py
msg.enc
msg.txt
문제의 아이디어는 숨겨진 키를 사용하여 flag.enc 파일을 해독하는 것입니다. Special_rsa.py 파일 암호화 및 암호 해독 프로세스를 읽은 후 숨겨진 키를 찾기 위해 간단한 공식을 만들었습니다.

의사 코드는 다음과 같습니다.
Flag.Sage:
n=2392741101402069577293491676495366164131014848097705645555098192491740356525 2406759062857005163575789294011455370097616796964364149615268689222802 84616866172935341157887779955597796504470493457574208747413571865964257536 6745526687040215455243999664444133327167444448489755194077512522049071328 64905644212653872233024108968710807517682409176093420991798421358513510597 6197087976870587680544488010579782938032659399723048092175922038446875271 800863146459981063251316212922335646760250809535658444405555329096159179573898 34381018137378015593755767450675441333198683799788355179333368220408887171313131L
C1=14548997380897265239778888482538130965189896618080906889522381091726761 464959572943383024428028270717629953894592890859128818839328900295082849152 12544807953647890131962401194031870733075585984967138324357097419990561178318 60370227156331690196655564392649528306986826960829410120348913586592199732730 93325988046929724149888738000562732175284348956498435870801300524405443770 3771424168108213045567568595093421362481860950131878368049777335361101840 781184563686310564952643373040897880146783912050552987820128568056163894 0103972453014256762321262678746567102568384572894437061228985071385621160886
C2=1279394279511003831972453187568693507469327176085954164034728751116483335 10175551535140302561528783646407905656538533190119654101539360975162497155401 6671160730478932343949538202167508319292084519621768885187852666570298833042 608868415133423965248695300633727825113879783246034751883691295368172069170 967975561364277514063333333333333333333333333333333919309002580172938717542522097273017191969232179822 9276732198521711602080244950295889575423330809978629818447683842952156 65734671829249323604032320696267130330613343686404010107775919754082071807 6053994489609112348295905485503118015857578928333063130781623152118126597
M1=824607418264209112557831182837484369942332438113476912293348292187007286240 47916518503687366611595562099039411430629666684708665972123162319995017758 424796091810259884653332576136128144958751327844746912646700735951818136352 29344430676552368048955009385252480130461232373542296281962196795304997110 0680121178300585729736293033898872451934860435975444221921351685973208209 8736239096292783211814850964460652986900587470909029831236523067172379085099 8541956664376820820570709272500330966205788986903967069502400197278640914 365182024141669020415892764617055978888961646422295827174937541993187360
m2=1557505145385852175310846206372375098638609306776394831661215794190835527333264120183706295101222781556841830916444 73080588354424242666669492434886916408150576082667777274000617262798719713774366282940252968282547129986182946 35106592585860207322283512582915279658297704895472058973840956731373225161616880937364049427129998716709088868 979602445850170570479910915276237360542684800524892130399203757308530033852905800033030https://63361251274293258
R1=1290067619162043036042711764185954751688135963316161667607569211546932766 9904794753733843243421023216854474678883988490943632029926246606328959443
R2=77189751594023896179244310011396751280131630286624078102368166185434662628 613443576470197777762407935675150925250347533339819819841265295767981059
_, A, B=XGCD (R1, R2)
k=pow ((C1/M1 % N), A, N) * Pow ((C2/M2 % N), B, N)
인쇄 (k)
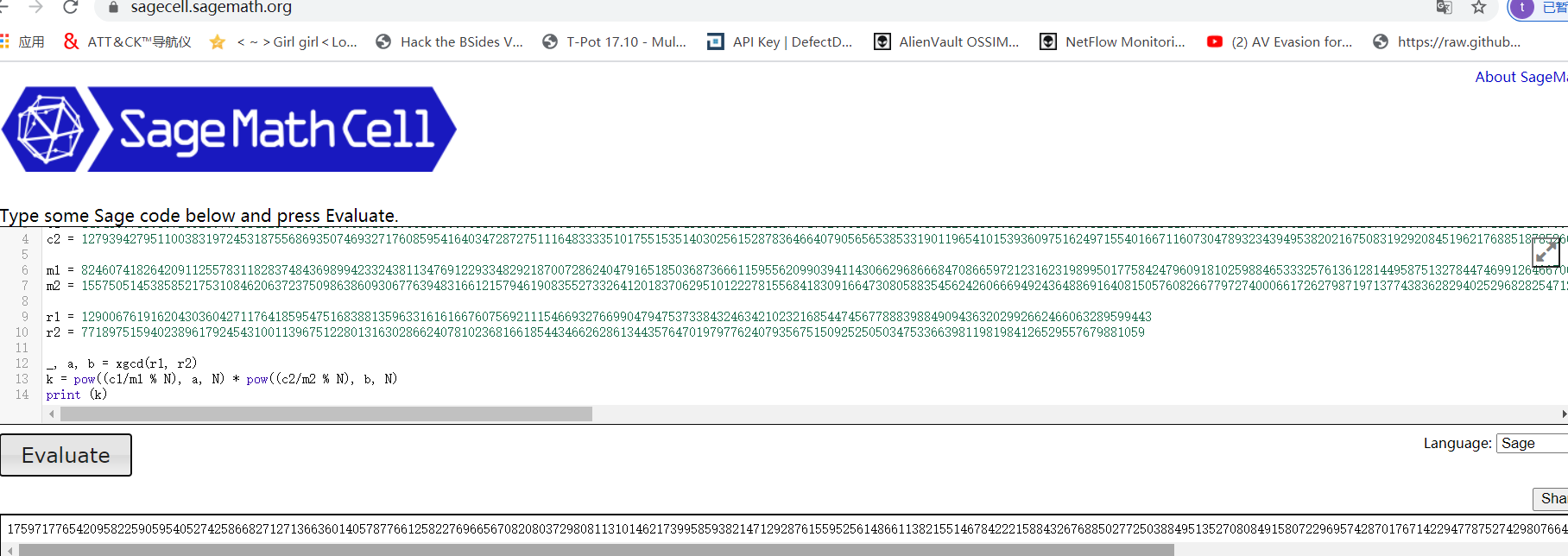
1759717765420958225905954052742586827127136360140578776125827666708208208 03729808113101462173958593821471292876155952561486138215146784222151584326 76885027725038849513527080849158072969574287017671429477875274298076436072 183367444762212399986777712409350161927351342180317734718106325421492111961
키를 얻으십시오, 해독 플래그 .enc, 답을 얻으십시오.
A==0: RETURN (B, 0, 1) ELSE: G, y, X=EGCD (B % A, A) RETURM (G, X- (B //a) * Y, Y) DEF MODINV (A, M) : G, X, y=EGCD (a,) mdef pad_even (x) : return ( '', '0') [len (x) 2] + xdef decrypt (c, k) : out='', msgpack.unpackb (c) : r=int (r_s.encode ( 'hex'), 16), 16) k_inv=modinv (k, n) out +=pad_even (format (pow (k_inv, r, n) * c % n, 'x'). decode ( 'hex') return outn=2392741101402069577293491676495366164131014848097705645555098192491740356525 2406759062857005163575789294011455370097616796964364149615268689222802 84616866172935341157887779955597796504470493457574208747413571865964257536 6745526687040215455243999664444133327167444448489755194077512522049071328 64905644212653872233024108968710807517682409176093420991798421358513510597 6197087976870587680544488010579782938032659399723048092175922038446875271 800863146459981063251316212922335646760250809535658444405555329096159179573898 3438101813737801559375576745067544133319868379978835179333368220408871313131K=175971776542095822590595405274258682712713636014057876125827696667082080 3729808113101462173958593821471292876155952561486611382151467842221584326768 85027725038495135270808491580722969474287017671429478752742980764360721833 674447621239998677712409350161927351342180317347181063254421492111961 프린트 decrypt (open ( 'flag.enc'). read (), k)
마침내 FLAG:을 얻었습니다
FLAG: BCTF {Q00000000000B333333333 -JU57 -W0N -PWN20WN !!!!
제목은 flag.enc와 public.pem을 제공하고 첨부 파일 다운로드 주소를 제공합니다.
OpenSSL을 설치하면 N 및 E를 읽을 수 있습니다. n은 크지 않기 때문에 yafu 또는 factordb.com에서 그것을 분해하여 n=p * q * r을 얻을 수 있습니다.
flag.enc에 따르면 암호 텍스트 m을 얻을 수 있습니다
중국 잔류 정리에 따르면, 우리는 p, q, r에서 나머지 m을 필요로하며 pmod, qmod, rmod로 설정 될 수 있습니다.
그런 다음 나머지 모드를 세 번, 즉 : proot ^ 3 ≡ pmod (mod p), find : proot, qroot, rroot에 대해서도 마찬가지입니다.
웹 도구를 사용하면 다음을 직접 계산할 수 있습니다.
x^3 = 193425633769363634263836075415482 (MOD 270381940535406199999045656363). - Wolfram|Alpha
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.
e=3
n=2329271097867038040364127327000284747060006568046290011918413375473934024039715180540887338067
Yafu를 사용하여 모듈러스를 다음으로 나눕니다.
P=2644061536395242196516853423447
Q=27038194053540661979045656526063
R=32581479300404876772405716877547
우리는 세 가지 소수를 얻습니다. 이것은 여전히 좋습니다. 단지 다중 품질의 RSA 일 수 있습니다. 이것은 전혀 놀라운 일이 아닙니다. 일반적으로, 그것은 매우 간단합니다 (P-1) (Q-1) (R-1), 나머지 계산은 평소와 같이 수행됩니다. 그러나 모듈 식 곱셈이 존재하지 않기 때문에 존재하지 않습니다. 그 이유는 분명합니다. GCD (E, Client)=3은 1이어야합니다. 이것은 우리가 비슷한 상황 (예 : https://github.com/p4-team/ctf/tree/mas
RSA 디코딩을 적용하기 전에이 3을 제거해야합니다. 이는 암호화가 다음과 같습니다.
ciphertext=plaintext^e mod n=(PlainText^e ')^3 mod n
따라서 방정식의 양쪽에 모듈러스 큐브 루트 (모드 N)를 형성 할 수 있다면 RSA 디코딩에 e '=e/3을 사용할 수 있습니다. E=3이므로 E '=E/3=1이므로 여기서 쉽지 않으므로 암호화가 간단하다는 것을 의미합니다.
ciphertext=plaintext^3 mod n
따라서, 전체 암호 해독 공정은 암호 텍스트에서 모드 큐브 루트 (mod n)를 요구한다.
곰팡이 뿌리에 대한 일부 독서는 이것이 가능하다는 결론으로 이어졌지만 제한된 영역에서만 가능합니다. 따라서 N으로는 할 수 없습니다. 복합 번호입니다. PQR이기 때문입니다.
이 질문은 정리 (https://en.wikipedia.org/wiki/chinese_remainder_theorem)를 상기시켜줍니다. 한동안 생각을 한 후, 우리는 암호 텍스트 (Mod Prime)에서 3 번의 3 번의 프라임의 3 회 금형 뿌리를 계산할 수 있다면 병합 루트를 계산할 수 있다는 생각을 생각해 냈습니다. 가우스 알고리즘 (http://www.di-mgt.com.au/crt.html#gaussalg)을 사용하여이를 달성 할 수 있습니다.
그래서 우리는 계속 계산합니다.
Pt^3 mod p=ciperhtext mod p=20827907981030303078407891583129
Pt^3 mod q=ciperhtext mod q=193425637693634263836075415482
Pt^3 mod r=ciperhtext mod r=1052528394777602788040671000
그런 다음 PT 의이 방정식을 해결하는 데 시간이 걸렸고 마지막으로 Wolframalpha 가이 기능을 구현한다는 것을 알았습니다.
x^3 = 2 - Wolfram|Alpha
Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.

